場合の数
場合の数とは、ある事柄に対して、全部で何通りの場合があるかを示します。
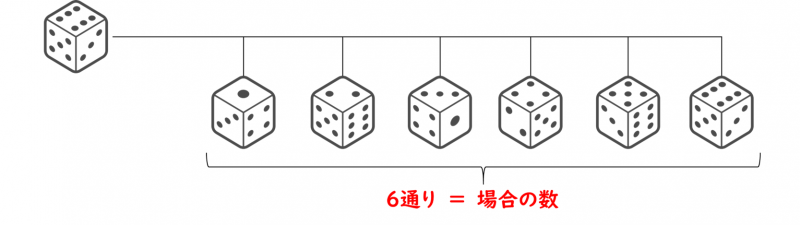
例えば、サイコロを1回振るときの場合の数は、出目が1~6なので、6通りになります。
このページでは、場合の数のうち『事柄が複数回起きる場合の数』と『複数の事柄が起きる場合の数』の2つの求め方を解説していきます。
| 用語 | 説明 |
|---|---|
| 場合の数 | ある事柄に対して、全部で何通りの場合があるかのこと |
| 事柄が複数回起きる場合の数 | m通りの事柄がN回起きるときの場合の数 \(m×m×・・・m※=m^N[通り]\) \(※mのN回(個)掛け算\) |
| 複数の事柄が起きる場合数 | 事柄A(m通り)とB(n通り)が起きる場合の数 \(m×n[通り]\) |
| 順列 | データの集まり(n個)から任意の個数(r個)を並べた際の、並べ方の場合の数 \(nPr=n×(n-1)×(n-2)×・・・×(n-r+1)\) |
| 組み合わせ | データの集まり(n個)から任意の個数(r個)を選ぶ、選び方の場合の数 \(nCr=nPr/r!\) [補足]r!(rの階乗):rから1までの数を全て掛け算 |
事柄が複数回起きる場合の数
『m通りの事柄がN回起きるときの場合の数』は次の式で表すことができます。
\(m×m×・・・m※=m^N[通り]\)
\(※mのN回(個)掛け算\)
具体例として、『コインを3回(個)投げるときの場合の数』を考えます。このとき、コインは表か裏の2通りなので、m=2[通り]となります。また、コインを3回(個)投げるので、N=3[回(個)]です。
したがって、場合の数は次のように計算できます。
\(m^N=2^3=8[通り]\)
つまり、コインを3回(個)投げるときの場合の数は、『8通り』です。この場合の数を樹形図(事柄を順番に書き出す表記法)でも確認しておきましょう。
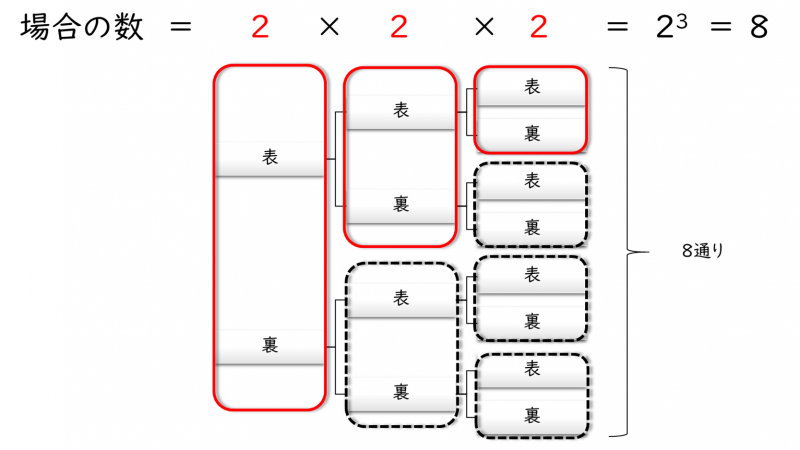
樹形図でも、場合の数は『8通り』と分かります。
【例題】事柄が複数回起きる場合の数
ITパスポート試験での『事柄が複数回起きる場合の数』の出題例を確認しておきましょう。
パスワードの解読方法の一つとして,全ての文字の組合せを試みる総当たり攻撃がある。
出典:平成26年秋期 問51
“0” から“9”の10種類の文字を使用できるパスワードにおいて,桁数を4桁から6桁に増やすと,総当たり攻撃でパスワードを解読するための最大の試行回数は何倍になるか。
ア:1.5
イ:20
ウ:100
エ:1024
総当たり攻撃の最大試行回数は、パスワードのパターン数に等しいです。したがい、4桁と6桁のパスワードのパターン数を場合の数として計算します。
1)4桁のパスワードのとき
・m通り:”0″ ~”9″→10通り
・N回(個):4桁→4個
\(・場合の数
=m^N=10^4[通り](①)\)
2)6桁のパスワードのとき
・m通り:”0″ ~”9″→10通り
・N回(個):6桁→6個
\(・場合の数
=m^N=10^6[通り](②)\)
6桁のパスワードの総当たり攻撃の最大試行回数が、4桁のパスワードの何倍かを計算するので、『6桁の最大試行回数』を『4桁の最大試行回数』で割ればよいです。
\(②÷①\)
\(=②/①\)
\(=10^6/10^4\)
\(=10^{6-4}\)
\(=10^2=100\)
したがって、ウ:100
複数の事柄が起きる場合の数
『事柄Aがm通り、事柄Bがn通りのとき、事柄AとBが起こる場合の数』は、次の式で表すことができます。
\(m×n[通り]\)
例えば、『コインとサイコロを1回(個)ずつ投げるときの場合の数』を考えてみましょう。
このとき、コインは表か裏の2通り、サイコロは、1~6の6通りになります。つまりm=2[通り]、n=6[通り]となります。
したがって、場合の数は次のように計算できます。
\(m×n=2×6=12[通り]\)
『コインとサイコロを1回(個)ずつ投げるときの場合の数』は『12通り』です。
この場合の数を樹形図で確認しておきましょう。
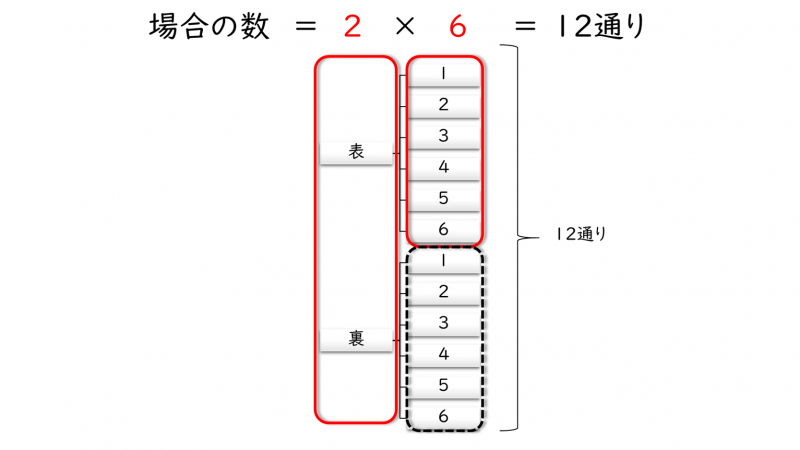
樹形図でも場合の数は『12通り』とであることが分かります。
【例題】複数の事柄が起きる場合の数
ITパスポート試験での『複数の事柄が起きる場合の数』出題例を確認しておきましょう。
次の体系をもつ電話番号において,80億個の番号を創出したい。番号の最低限必要な桁数は幾つか。ここで,桁数には”020″を含むこととする
出典:令和元年秋期 問82
020①②…②
①:1~3及び5~9のいずれかを指定
②:各桁に0~9のいずれかを指定
ア:11 イ:12 ウ:13 エ:14
電話番号の①の部分と②…②の部分のパターン数を場合の数としてそれぞれ求めます。まず、m通りの事柄がN回起きる場合の数の式(\(m^N\))を用います。
①の部分)
・m通り:1~3及び5~9→8通り
・N回(個):1個
・場合の数\(=m^N=8^1=8[通り]\)
②…②の部分)
・n通り:0~9→10通り
・N回(個):N回(Nは不明)
・場合の数\(=10^N[通り]\)
①の部分(8通り=m通り)と②…②( \(10^N[通り]\)=n通り)と求められました。
電話番号の場合の数は、事柄A(m通り)とB(n通り)が起きる場合の数の式(\(m×n[通り]\))を用いて次のように求めることができます。
\(m×n=8×10^N[通り]\)
また、問題文より、\(8×10^N[通り]\)が80億より大きくなれば良いので、
\(8×10^N ≧80億\)
\(8×10^N ≧8×10^9\)
\(N≧9\)
\([補足]10億=1,000,000,000=10^9\)
つまり、②が9個以上あればよいので、最低限必要な番号は次のような形になる。
020『①』『②×9』
したがって、イ:12桁(3桁+1桁+9桁)と最低限必要となる。
【まとめ】確率と統計(場合の数)
それでは最後におさらいをします。場合の数を式から求められるように頭の中を整理しておきましょう!
| 用語 | 説明 |
|---|---|
| 場合の数 | ある事柄に対して、全部で何通りの場合があるかのこと |
| 事柄が複数回起きる場合の数 | m通りの事柄がN回起きるときの場合の数 \(m×m×・・・m※=m^N[通り]\) \(※mのN回(個)掛け算\) |
| 複数の事柄が起きる場合数 | 事柄A(m通り)とB(n通り)が起きる場合の数 \(m×n[通り]\) |




コメント