・分散:平均値からのデータのばらつきを表す値
・標準偏差:平均値からのデータのばらつきを表す値、分散の平方根で計算
・偏差値:テストの成績が、受験者全体のどの程度かを表す値
分散/標準偏差/偏差値とは?
データのばらつきを表現する値として、「分散」「標準偏差」「偏差値」について解説します。
分散
分散とは、平均値からのデータのばらつきを表す値です。
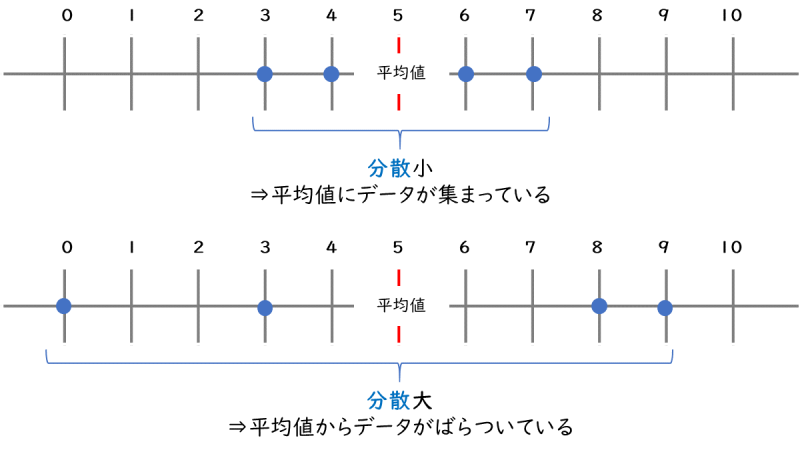
分散が小さいほど、平均値にデータが集まっていることを表します。一方、分散が大きいほど、平均値からデータがばらついていることになります。
分散は、次の計算式で求めることができます。
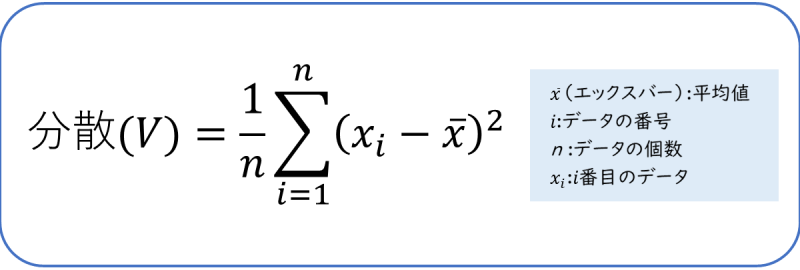
この計算式の意味を確認していきます。
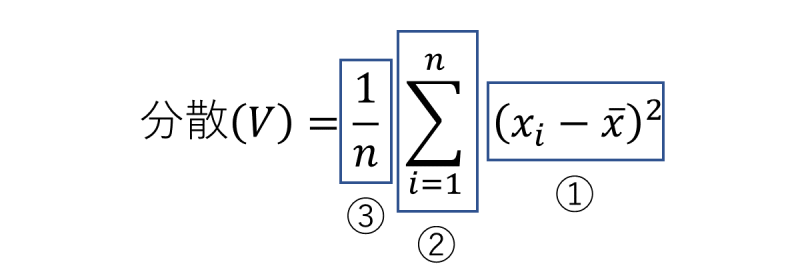
②:①の値の合計を計算
③:②の値をデータ数(n)で割る
つまり、分散は「平均値と各データの差分を2乗した値の平均値」の計算に等しくなります。
次のテストの点数を例に、分散を計算してみます。
| 氏名 | 点数\((x^i)\) | ①:\((x^i-\bar x)^2\) |
|---|---|---|
| Aさん | 60 | 36 |
| Bさん | 90 | 576 |
| Cさん | 100 | 1156 |
| Dさん | 70 | 16 |
| Eさん | 60 | 36 |
| Fさん | 60 | 36 |
| Gさん | 40 | 676 |
| Hさん | 80 | 196 |
| Iさん | 70 | 16 |
| Jさん | 30 | 1296 |
| 合計 | 660 | ②:4040 |
| 平均 | 66 | ③:404 |
| 分散\((V)\) | - | 404 |
したがって、分散は「404」となることが分かります。
標準偏差
標準偏差もデータのばらつきを表す値です。
分散と同様、標準偏差が小さいほど、データが平均値に集まっていることになります。逆に標準偏差が大きいほど、平均値からデータがばらついていることを表します。
標準偏差は、分散の平方根(ルート)を計算した値になります。
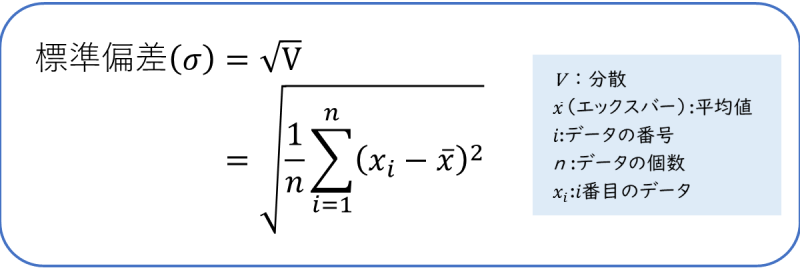
標準偏差の計算式の意味を確認していきましょう。
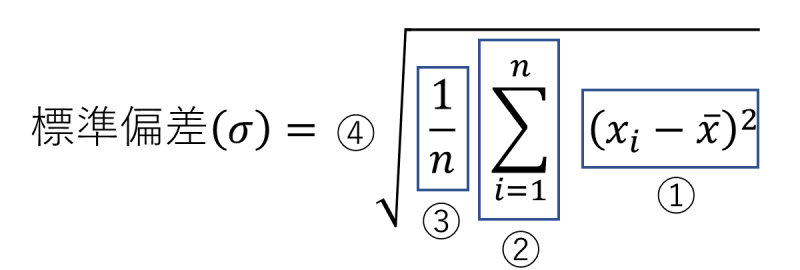
②:①の値の合計を計算
③:②の値をデータ数(n)で割る
④:③の平方根をとる
テストの点数を例に、標準偏差を計算してみます。
| 氏名 | 点数\((x^i)\) | ①:\((x^i-\bar x)^2\) |
|---|---|---|
| Aさん | 60 | 36 |
| Bさん | 90 | 576 |
| Cさん | 100 | 1156 |
| Dさん | 70 | 16 |
| Eさん | 60 | 36 |
| Fさん | 60 | 36 |
| Gさん | 40 | 676 |
| Hさん | 80 | 196 |
| Iさん | 70 | 16 |
| Jさん | 30 | 1296 |
| 合計 | 660 | ②:4040 |
| 平均 | 66 | ③:404 |
| 分散\((V)\) | - | 404 |
| 標準偏差\((σ)\) (平方根) | - | ④:20.1 |
したがって、標準偏差は「20.1」と計算することができました。
[補足]分散と標準偏差の単位
分散も標準偏差もデータのばらつきを表す指標ですが、分散と標準偏差では、単位の次元が異なります。
具体的には、分散はデータの単位の2乗、標準偏差の単位は、元データと同じ(1乗)になります。この理由は、分散がデータの差分を2乗して計算することに対し、標準偏差は分散の平方根をとるためです。
標準偏差は、元データとの単位の次元が等しいため、ばらつきを表現する指標として多く利用されます。
偏差値
偏差値とは、自分のテストの点数が、受験者全体のどの程度かを表す値です。
偏差値「50」を閾値に、平均点よりも高い、低いが決定します。
偏差値=50:平均点と同じ
偏差値<50:平均点より低い
偏差値は次の計算で求めることができます。
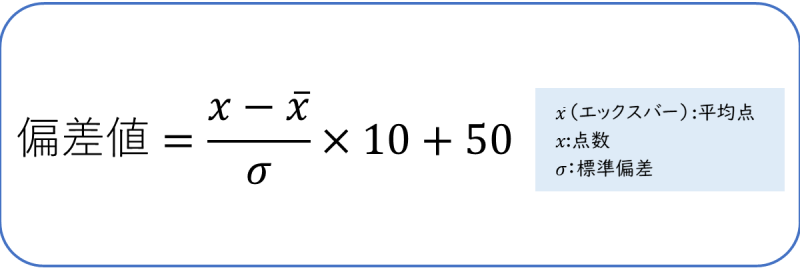
偏差値の計算式を確認していきます。
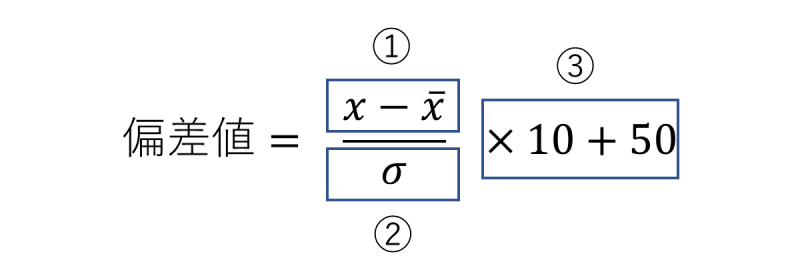
②:①を標準偏差で割る
③:②に10を掛け、50を足す
実際に、偏差値を計算してみましょう。
| 氏名 | 点数\((x^i)\) | ①:\((x^i-\bar x)\) | ②:\(①/σ\) | 偏差値 ③:\(②×10+50\) |
|---|---|---|---|---|
| Aさん | 60 | -6 | -0.3 | 47 |
| Bさん | 90 | 24 | 1.19 | 61.9 |
| Cさん | 100 | 34 | 1.69 | 66.9 |
| Dさん | 70 | 4 | 0.2 | 52 |
| Eさん | 60 | -6 | -0.3 | 47 |
| Fさん | 60 | -6 | -0.3 | 47 |
| Gさん | 40 | -26 | -1.29 | 37.1 |
| Hさん | 80 | 14 | 0.7 | 57 |
| Iさん | 70 | 4 | 0.2 | 52 |
| Jさん | 30 | -36 | -1.79 | 32.1 |
| 合計 | 660 | - | - | - |
| 平均 | 66 | - | - | - |
| 分散\((V)\) | 404 | - | - | - |
| 標準偏差\((σ)\) | 20.1 | - | - | - |
テストの平均点は「66点」なので、「点数が66点より高いの人は偏差値が50より高く」、「66点より低い人は、偏差値が50より低く」なると分かります。
【まとめ】分散/偏差/標準偏差
それでは最後におさらいをしておきましょう!
| 用語 | 説明 |
|---|---|
| 分散 | 平均値からのデータのばらつきを表す値 \(V={1 \above 1pt n}\sum{_{i=1}^n}(x^i-\bar x)\) |
| 標準偏差 | 平均値からのデータのばらつきを表す値 分散の平方根で計算 \(σ= \sqrt {{1 \above 1pt n}\sum{_{i=1}^n}(x^i-\bar x)}\) |
| 偏差値 | テストの成績が、受験者全体のどの程度かを表す値 偏差値>50:平均点より高い 偏差値=50:平均点と同じ 偏差値<50:平均点より低い \(偏差値={x^i-\bar x \above 1pt σ}×10+50\) |



.png)
コメント