論理演算と真理値表とは?
論理演算とは、0または1(2進数1桁)の入力に対して、出力を計算する演算です。
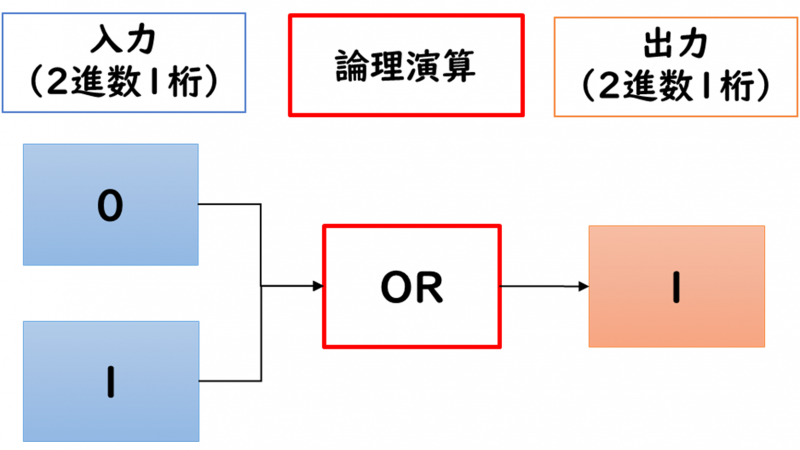
また、論理演算の入力と出力をまとめた表を真理値表と呼びます。下表は、2AとBの2つを入力し、出力した場合の真理値表の例です。
| 入力 A | 入力 B | 出力 \(A + B\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
OR(論理和)/AND(論理積)/NOT(論理否定)/ XOR(排他的論理和)
論理演算には、『OR(論理和)』、『AND(論理積)』、『NOT(論理否定)』、『XOR(排他的論理和)』の4種類があります。
| 用語 | 説明 |
|---|---|
| OR(論理和) | 入力のどちらか一方が1であれば、出力が1になる論理演算 論理式:\(A+B\) |
| AND(論理積) | 入力の両方が1であれば、出力が1になる論理演算 論理式:\(A・B\) |
| NOT(論理否定) | 入力を反転させて出力する論理演算 論理式:\(\bar A\) |
| XOR(排他的論理和) | 入力が異なる場合、出力が1になる論理演算 論理式:\(\bar A・B+A・\bar B\) |
OR(論理和)
OR(論理和)は、入力のどちらか一方が1であれば、出力が1になる論理演算です。
論理式では『\(A+B\)』と記述します。
| 入力 A | 入力 B | 出力 \(A + B\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
OR(論理和)は、和集合(AまたはB)のベン図と対比して理解しておきましょう。
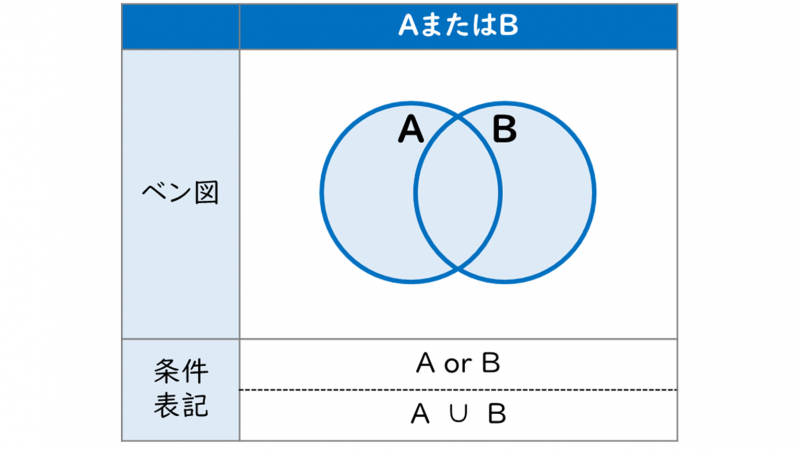
集合とベン図についての詳細は、『33-04.集合(和集合/積集合/否定)とベン図』を確認しましょう。
AND(論理積)
AND(論理積)は、入力の両方が1であれば、出力が1になる論理演算です。
論理式では『\(A・B\)』と記述します。
| 入力 A | 入力 B | 出力 \(A ・ B\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
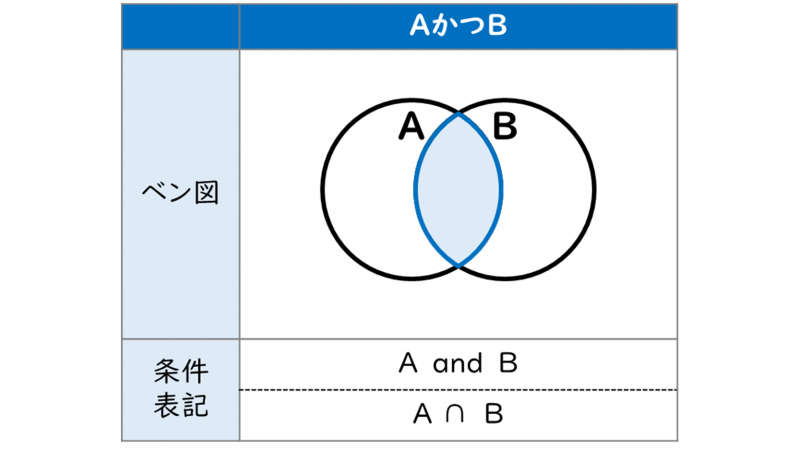
AND(論理積)は、積集合(AかつB)のベン図と対比して確認をしておきます。
NOT(論理否定)
NOT(論理否定)は、入力を反転させて出力する論理演算です。入力が1のときは、出力が0となり、入力が0のときは、出力が1となります。
論理式では、『\(\bar A\)』と記述します。
| 入力 A | 出力 \(\bar A\) |
|---|---|
| 0 | 1 |
| 1 | 0 |
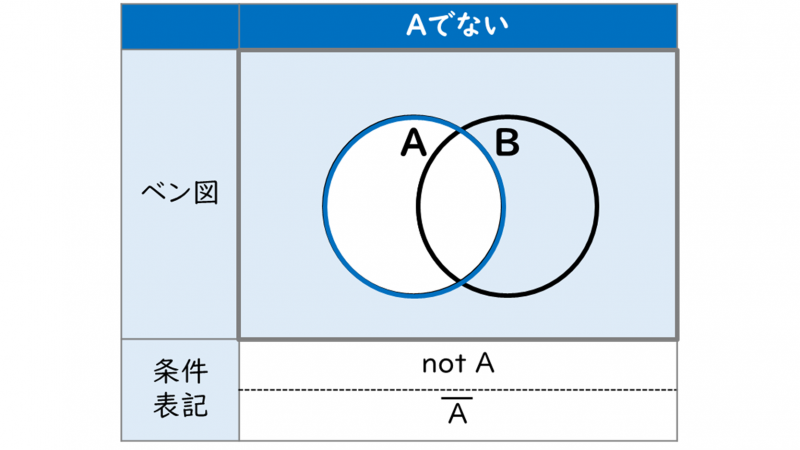
NOT(論理否定)と否定の集合と比較します。
XOR(排他的論理和)
XOR(排他的論理和)は、入力が異なる場合、出力が1になる論理演算です。OR(論理和)のA=1、B=1のときの出力=1が除外(排他)され、出力=0になるため、XOR(排他的論理和)と呼ばれます。
論理式では、『\(\bar A・B+A・\bar B\)』と記述します。
| 入力 A | 入力 B | 出力 \(\bar A・B+A・\bar B\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
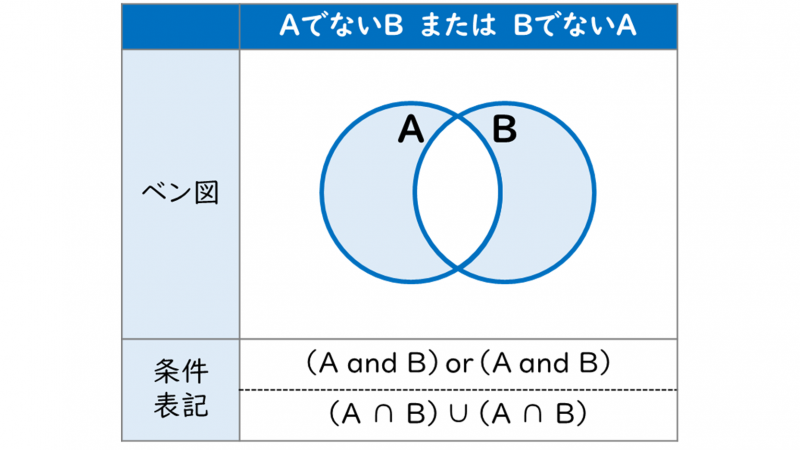
\(\bar A・B+A・\bar B\)の対比として、『\(\bar A ∪ B+A ∪ \bar B\)』の集合をベン図で表すと次のようになります。
【まとめ】論理演算
それでは最後におさらいをしておきましょう。
| 用語 | 説明 |
|---|---|
| 論理演算 | 0または1(2進数1桁)の入力に対して、出力を計算する演算 |
| 真理値表 | 論理演算の入力と出力の関係をまとめた表 |
| OR(論理和) | 入力のどちらか一方が1であれば、出力が1になる論理演算 論理式:\(A+B\) |
| AND(論理積) | 入力の両方が1であれば、出力が1になる論理演算 論理式:\(A・B\) |
| NOT(論理否定) | 入力を反転させて出力する論理演算 論理式:\(\bar A\) |
| XOR(排他的論理和) | 入力が異なる場合、出力が1になる論理演算 論理式:\(\bar A・B+A・\bar B\) |




コメント