33-02.数と表現（基数変換）

基数とは？
基数変換とは？
【まとめ】数の表現（基数変換）

基数とは？

基数とは、1桁で表現できる数のことです。

具体的に、2進数は1桁で『0』と『1』の2つの数を表現できるので、基数は『2』です。同様に、10進数、8進数、16進数の基数はそれぞれ、10、8､16になります。つまり、N進数の基数はNです。

基数変換とは？

2進数から10進数など、別の基数の進数に変換することを基数変換と呼びます。

※以降、基数がNのN進数を $（●）_N$ で表記します。

2進数からN進数（10進数/8進数/16進数）への基数変換

2進数からN進数（10進数/8進数/16進数）への基数変換は、次の計算により実施します。

基数変換前	基数変換後	基数変換の方法
２進数	１０進数	一の位から順に2^0, 2^1,2^3・・・を掛けて足し算 ※2^n：2のn乗
	８進数	『３桁』に区切り、２進数→１０進数→８進数に変換
	１６進数	『４桁』に区切り、２進数→１０進数→１６進数に変換

2進数から10進数への基数変換

2進数から10進数への基数変換は、2進数の一の位から順に $2^0、2^1、2^3・・・$ を掛けて足し算をします。

$(1001)_2 \\~→(2^0×1)+(2^1×0)+(2^2×0)+(2^3×1) \\~=(1×1)+(2×0)+(4×0)+(8×1) \\~=1+0+0+8 \\~=(9)_{10}$

2進数から8進数への基数変換

2進数から8進数への基数変換は、2進数を一の位から『3桁』で区切り、2進数→10進数→8進数に変換し、数字を合わせます。

2進数を3桁で区切った際に、足りない桁は0で補います。

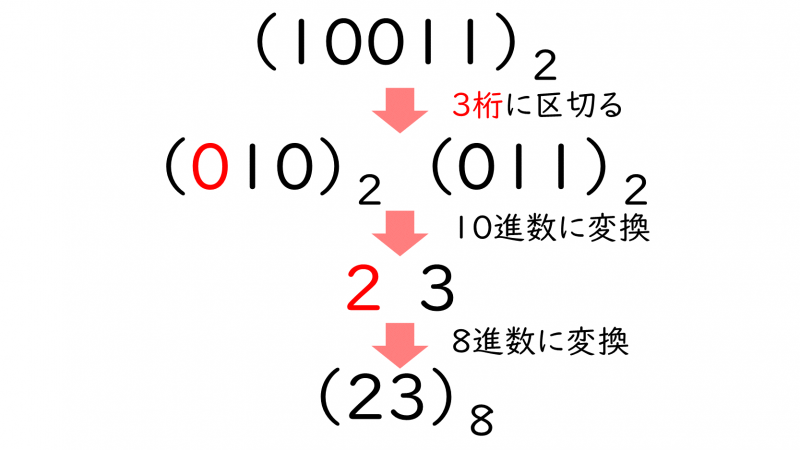
$(011)_2 \\~→(2^0×1)+(2^1×1)+(2^2×0) \\~=(1×1)+(2×1)+(4×0) \\~=1+2+0 \\~=(3)_{10} \\~=(3)_{8}・・・①$

$(010)_2 \\~→(2^0×0)+(2^1×1)+(2^2×0) \\~=(1×0)+(2×1)+(4×0) \\~=0+2+0 \\~=(2)_{10} \\~=(2)_{8}・・・②$

したがって、①と②の数字を合わせると、
$(10011)_2＝(23)_8$
となる。

10進数から8進数への基数変換が分からない場合は、『33-01.数と表現（2進数/10進数/8進数/16進数）』の関係表を復習しましょう。

2進数から16進数への基数変換

2進数から16進数への基数変換は、2進数をーの位から『4桁』で区切り、2進数→10進数→16進数に変換し、数字を合わせます。

2進数を4桁で区切った際に、足りない桁は0で補います

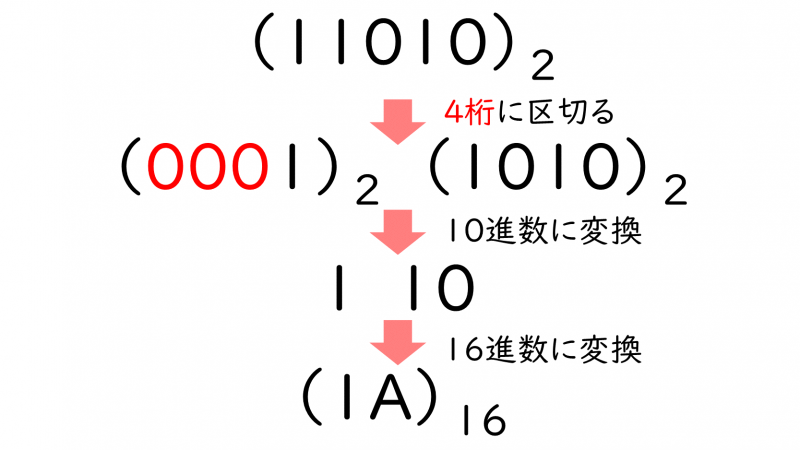
$(1010)_2 \\~→(2^0×0)+(2^1×1)+(2^2×0)+(2^3×1) \\~=(1×1)+(2×1)+(4×0)+(8×1) \\~=0+2+0+8 \\~=(10)_{10} \\~=(A)_{16}・・・①$

$(0001)_2 \\~→(2^0×1)+(2^1×0)+(2^2×0)+(2^3×0) \\~=(1×1)+(2×0)+(4×0)+(8×1) \\~=1+0+0+0 \\~=(1)_{10} \\~=(1)_{16}・・・①$

したがって、①と②の数字を合わせると、
$(11010)_2＝(1A)_{16}$
となる。

10進数から16進数への基数変換が分からない場合は、『33-01.数と表現（2進数/10進数/8進数/16進数）』の関係表を復習しましょう。

N進数（10進数/8進数/16進数）から2進数への基数変換

N進数から2進数への基数変換は、次の計算により実施します。

基数変換前	基数変換後	基数変換の方法
１０進数	２進数	２で割り、最後の商と余りを並べる
８進数		８進数の１桁を『３桁』の２進数に変換し、数字を合わせる
１６進数		１６進数の１桁を『４桁』の２進数に変換し、数字を合わせる（A～Fは、１０進数に置き換え、2進数に変換）

10進数から2進数の基数変換

10進数から2進数の基数変換には、10進数を2で割り続けた余りと最後の商を一の位から順番に並べます。

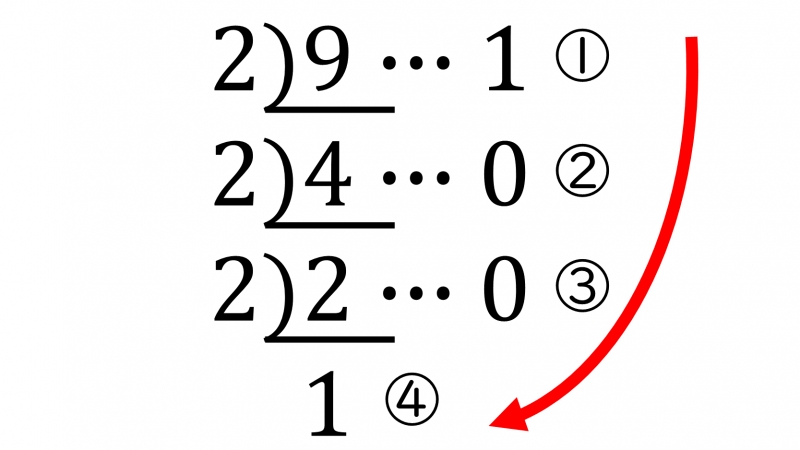
$9÷2=4~余り 1・・・① \\4÷2=2~余り 0・・・② \\2÷2=1(④)~ 余り 0・・・③$

したがって、
$(9)_{10}=(④③②①)_2=(1001)_2$

8進数から2進数の基数変換

8進数から2進数への基数変換は、8進数の1桁→10進数→『3桁』の2進数に変換し、数字を合わせます。

8進数の1桁を2進数に基数変換した際に、足りない桁は０で補います。

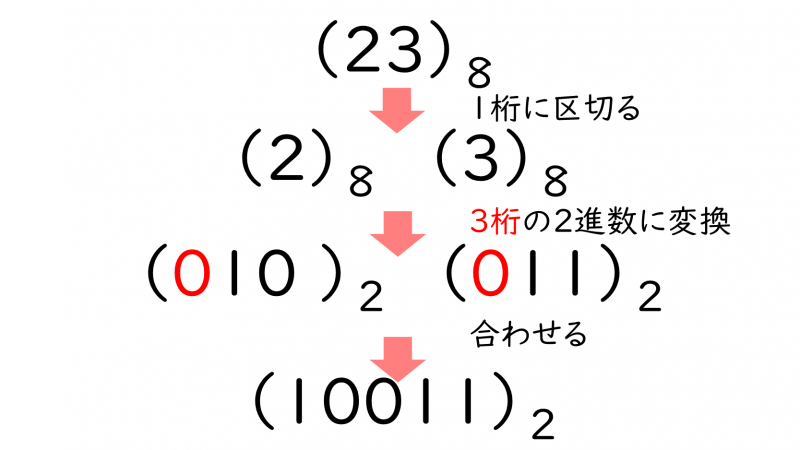
$(3)_8=(3)_{10} \\3÷2=1(②)~余り 1・・・①$
よって、

$(3)_8=(0②①)=(011)_2$

$(2)_8=(2)_10 \\2÷2=1(②)~余り 0・・・①$
よって、
$(3)_8=(0②①)=(010)_2$

したがって、
$(23)_8 =(010011)_2=(10011)_2$

16進数から2進数の基数変換

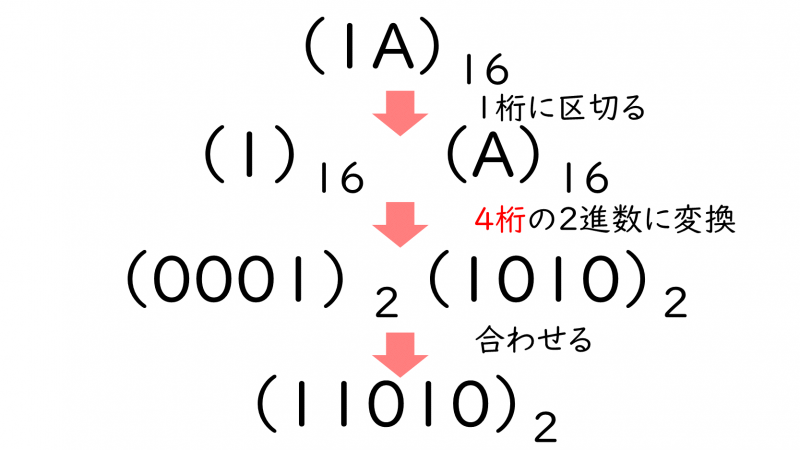
16進数から2進数への基数変換は、16進数の1桁→10進数→『4桁』の2進数に変換し、数字を合わせます。

$(A)_{16}=(10)_{10} \\10÷2=5 ~余り 0・・・① \\5÷2=2 ~余り 1・・・② \\2÷2=1 (④)~余り 0・・・③$
よって、

$(A)_{16}=(④③②①)_2=(1010)_2$

$(1)_{16}=(1)_{10} \\1÷2=0(②)~余り 1・・・①$
よって、
$(1)_{16}=(00②①)=(0001)_2$

したがって、
( $1A)_{16}=(00011010)_2=(11010)_2$

【補足】2進数の小数→10進数

2進数の小数から10進数への基数変換には、2進数の小数第一位から順に、 $2^{-1} 、2^{-2} 、2^{-3}・・・$ を掛けて足し算します。

$(11.101)_2 \\~→(2^1×1)+(2^0×1)+(2^{-1}×1)+(2^{-2}×0)+(2^{-3}×1) \\~=(2×1)+(1×1)+(0.5×1)+(0.25×1)+(0.125×1) \\~=2+1+0.5+0+0.125 \\~=(3.625)_{10}$

【まとめ】数の表現（基数変換）

それでは最後におさらいをしておきましょう。

基数変換前	基数変換後	基数変換の方法
２進数	１０進数	一の位から順に2^0, 2^1,2^3・・・を掛けて足し算 ※2^n：2のn乗
	８進数	『３桁』に区切り、２進数→１０進数→８進数に変換
	１６進数	『４桁』に区切り、２進数→１０進数→１６進数に変換
１０進数	２進数	２で割り、最後の商と余りを並べる
８進数		８進数の１桁を『３桁』の２進数に変換し、数字を合わせる
１６進数		１６進数の１桁を『４桁』の２進数に変換し、数字を合わせる（A～Fは、１０進数に置き換え、2進数に変換）