34-08.回帰分析（目的変数/説明変数/推定）

回帰分析（目的変数/説明変数）とは？

回帰分析とは、データの関係性を数式で表す分析です。

例えば、「身長」と「体重」のデータの関係性が、次のグラフであったと仮定します。

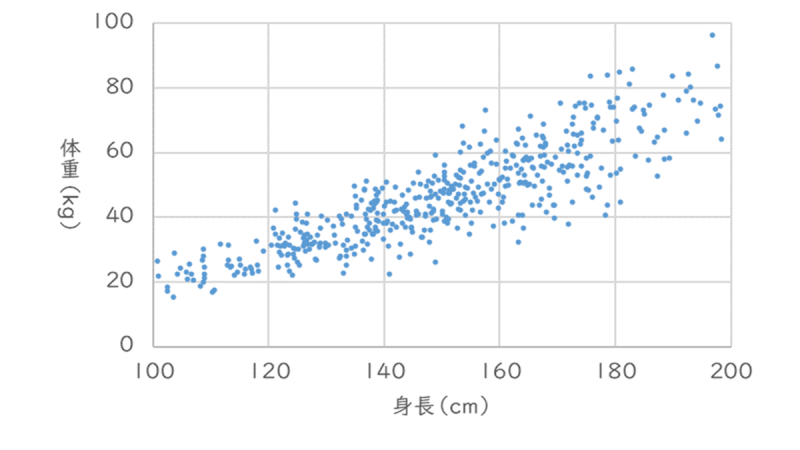
このとき、「身長」と「体重」をそれぞれ変数「x」と「y」とします。回帰分析では、この２つの変数間の関係性を、最も近しい思われる数式として記述することを考えます。

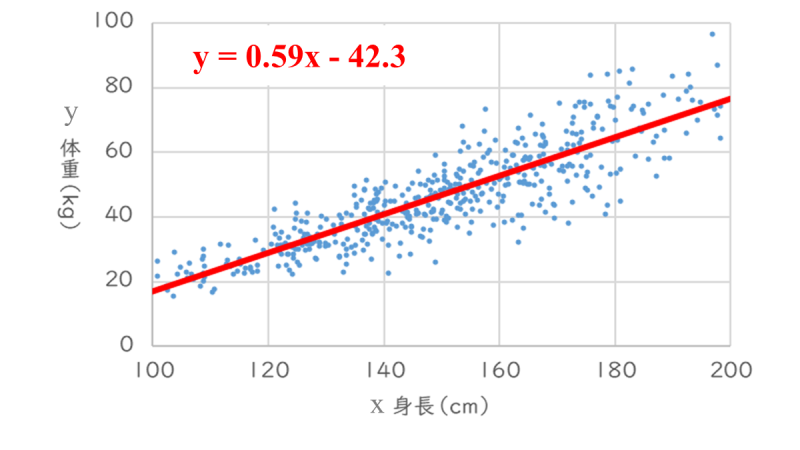
計算方法はのちほど補足しますが、今回の「身長（x）」と「体重（y）」では、「\(y = 0.59 x – 42.3\)」と計算できました。

繰返しになりますが、このようにデータの関係性を数式で表すことが、回帰分析です。

目的変数/説明変数

目的変数とは、回帰分析において数式で記述される側の変数です。先ほどの例では、変数「y」にあたる「体重」が目的変数になります。

一方、目的変数を表現するために用いた変数が、説明変数になります。したがい、変数「x」にあたる「身長」が説明変数です。

つまり、回帰分析とは、「目的変数」を「説明変数」による数式として記述することと言えます。

［補足］最小二乗法

最小二乗法とは、回帰分析で導出する「y=ax+b」における最も簡単なaとbを求める方法です。

具体的には、次の計算式（誤差の2乗の総和）が最小となるaとbを算出します。

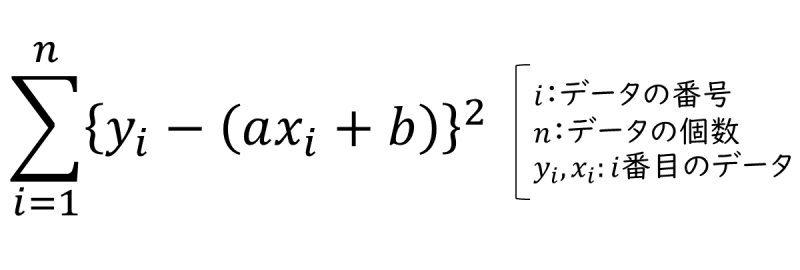
ITパスポート試験では、最小二乗法は出題範囲外ですが、より詳しく知りたい方は、下記の統計学を扱ったサイトを参考にしてください。

推定

推定とは、未知の変数の値を計算により見積もることです。回帰分析で考えると、未知の「目的変数」の値を既知の「説明変数」の値で計算することが推定といえます。

例えば、「身長 x=170[cm]」の場合における、「体重」の推定で考えます。

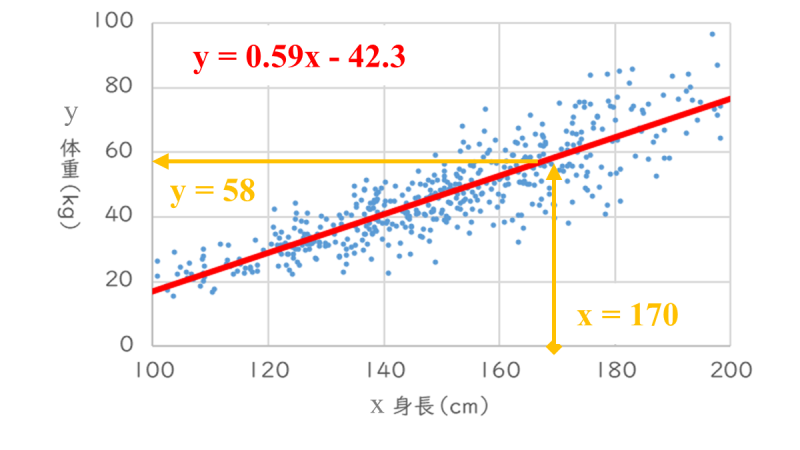
先ほど回帰分析で導出した計算式「\(y = 0.59 x – 42.3\)」に「x=170[cm]」を代入すると、「y=58[kg]」と計算できます。この計算結果が体重を推定した値となります。

なぜなら、回帰分析で導出した計算式は、「体重」と「身長」の関係性として、最も近しいとされるので、見積りとしては確からしさがあるためです。

このように、回帰分析の結果を用いて、未知の「目的変数」の値を既知の「説明変数」の値で計算することが推定になります。

【まとめ】回帰分析（目的変数/説明変数/推定）

それでは最後におさらいをしておきましょう！

用語	説明
回帰分析	データの関係性を数式で表すこと 目的変数を説明変数による数式で表す
目的変数	回帰分析において数式で記述される側の変数
説明変数	回帰分析において目的変数を表すための変数
推定	未知の変数の値を計算により見積もること