順列とは?
場合の数の考え方の1つに順列があります。順列は、データの集まりから任意の個数を並べた際の並べ方の総数です。
| 用語 | 説明 |
|---|---|
| 場合の数 | ある事柄に対して、全部で何通りの場合があるかのこと |
| 事柄が複数回起きる場合の数 | m通りの事柄がN回起きるときの場合の数 \(m×m×・・・m※=m^N[通り]\) \(※mのN回(個)掛け算\) |
| 複数の事柄が起きる場合数 | 事柄A(m通り)とB(n通り)が起きる場合の数 \(m×n[通り]\) |
| 順列 | データの集まり(n個)から任意の個数(r個)を並べた際の、並べ方の場合の数 \(nPr=n×(n-1)×(n-2)×・・・×(n-r+1)\) |
| 組み合わせ | データの集まり(n個)から任意の個数(r個)を選ぶ、選び方の場合の数 \(nCr=nPr/r!\) [補足]r!(rの階乗):rから1までの数を全て掛け算 |
全体n個からr個並べる順列を\({}_nP_r\)と記述し、次のように計算できます。
※P:Permutation(順列)
全体n個からr個並べる順列
\({}_nP_r=n×(n-1)×(n-2)×・・・×(n-r+1)\)
\({}_nP_r=n×(n-1)×(n-2)×・・・×(n-r+1)\)
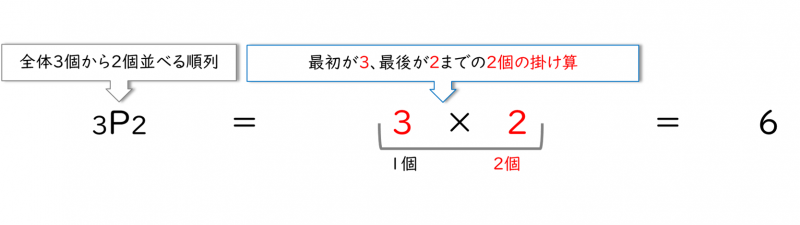
この公式は『全体がn個からr個並べる順列(\({}_nP_r\))』は、『最初がn、最後が(n-r+1)までのr個の掛け算』で求められると意味しています。

具体的に、Aさん・Bさん・Cさんの3人から、2人並べ、1番目がリーダー、2番目が副リーダーになる場合の順列を考えます。
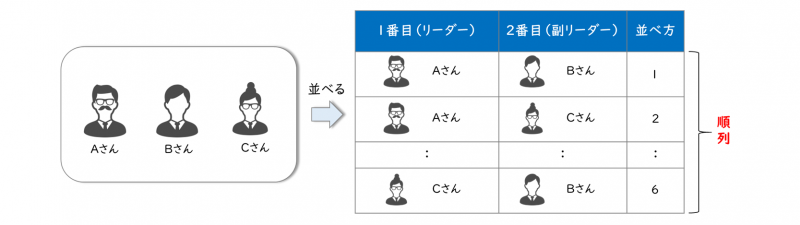
このとき、Aさん・Bさん・Cさん3人から2人並べる順列は次のように計算できます。
3人から2人並べる順列
\({}_3P_2=3×2=6通り\)
\(・n(全体の個数)=3\)
\(・r(並べる個数)=2\)
\(・n-r+1(最後の数)=3-2+1=2\)
\({}_3P_2=3×2=6通り\)
\(・n(全体の個数)=3\)
\(・r(並べる個数)=2\)
\(・n-r+1(最後の数)=3-2+1=2\)
この式は、『全体が3個から2個並べる順列(\({}_3P_2\))』は、『最初が3、最後が2(3-2+1)までの2個の掛け算』により『6通り』と求められることを意味しています。
この具体例を樹形図(事柄を順番に書き出す表記法)でも確認をしておきましょう。
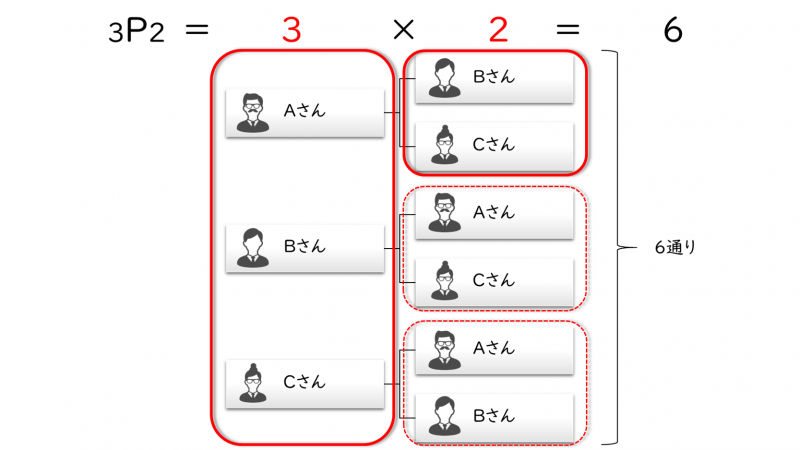
樹形図でも同様に、『6通り』であることが分かります。
【例題】順列
ITパスポート試験での『順列』の出題例を確認しておきましょう。
a、b、c、d、e、fの6文字を任意の順で1列に並べたとき、aとbが隣同士になる場合は、何通りか。
ア:120
出典:平成26年春期 問63
イ:240
ウ:720
エ:1,440
【解答・解説】
aとbが隣合わせになるのは、①(ab)、②(ba)と並んだ2つの場合があります。それぞれの場合の順列を考えます。
aとbが隣合わせになるのは、①(ab)、②(ba)と並んだ2つの場合があります。それぞれの場合の順列を考えます。
①(ab)と並ぶ場合
(ab)を1つの文字として考えればよいので、(ab) 、c、d、e、fの5文字を全て並べる順列を計算すると、
\({}_5P_5=5×4×3×2×1=120[通り]\)
②(ba)と並ぶ場合
①と同様に、(ab)を1つの文字として考えればよいので、(ba) 、c、d、e、fの5文字を全て並べる順列を計算すると、
\({}_5P_5=5×4×3×2×1=120[通り]\)
よって、①と②より
\(120+120=240[通り]\)
したがって、正解はイ:240となります。
【まとめ】確率と統計(順列)
それでは、最後におさらいをしておきましょう!
| 用語 | 説明 |
|---|---|
| 順列 | データの集まり(n個)から任意の個数(r個)を並べた際の、並べ方の場合の数 \({}_nP_r=n×(n-1)×(n-2)×・・・×(n-r+1)\) ※最初がn、最後が(n-r+1)までのr個の掛け算 |




コメント