組み合わせとは?
場合の数の考え方の1つに組み合わせがあります。組み合わせとは、データの集まりから任意の個数を選ぶ、選び方の総数です。
| 用語 | 説明 |
|---|---|
| 場合の数 | ある事柄に対して、全部で何通りの場合があるかのこと |
| 事柄が複数回起きる場合の数 | m通りの事柄がN回起きるときの場合の数 \(m×m×・・・m※=m^N[通り]\) \(※mのN回(個)掛け算\) |
| 複数の事柄が起きる場合数 | 事柄A(m通り)とB(n通り)が起きる場合の数 \(m×n[通り]\) |
| 順列 | データの集まり(n個)から任意の個数(r個)を並べた際の、並べ方の場合の数 \(nPr=n×(n-1)×(n-2)×・・・×(n-r+1)\) |
| 組み合わせ | データの集まり(n個)から任意の個数(r個)を選ぶ、選び方の場合の数 \(nCr=nPr/r!\) [補足]r!(rの階乗):rから1までの数を全て掛け算 |
全体n個からr個を選ぶ組み合わせを\({}_nC_r\)と記述し、次の式で表すことができます。
※C: Combination(組み合わせ)
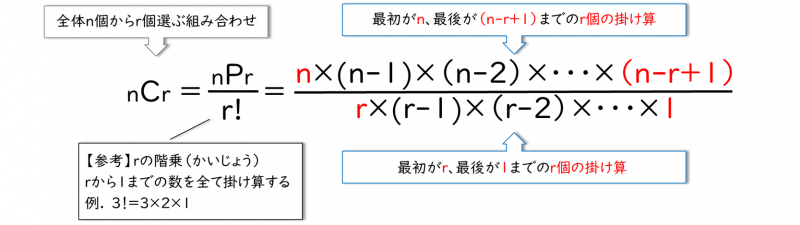
全体n個からr個を選ぶ組み合わせ
\({}_nC_r=\)\({}_nP_r \above 1pt r! \)\(=\)\(n×(n-1)×(n-2)×・・・×(n-r+1) \above 1pt r×(r-1)×(r-2)×・・・×1\)
※r!:rの階乗(かいじょう)
rから1までの数を全て掛け算する
例.3!=3×2×1
\({}_nC_r=\)\({}_nP_r \above 1pt r! \)\(=\)\(n×(n-1)×(n-2)×・・・×(n-r+1) \above 1pt r×(r-1)×(r-2)×・・・×1\)
※r!:rの階乗(かいじょう)
rから1までの数を全て掛け算する
例.3!=3×2×1
この公式は、『全体n個からr個を選ぶ組み合わせ(\({}_nC_r\))』は、『全体n個からr個並べる順列(\({}_nP_r\))』を『rの階乗(r!)』で割り求められると意味します。
また、分子は\({}_nP_r\)なので、『最初がn、最後が(n-r+1)までのr個の掛け算』を、分母はr!なので、『最初がr、最後が1までのr個の掛け算』になります。
具体的に、Aさん・Bさん・Cさんの3人から、2人選ぶ場合の組み合わせを考えます。
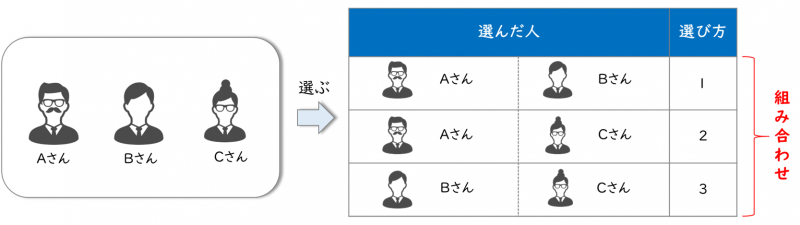
このとき、Aさん・Bさん・Cさんの3人から、2人選ぶ場合の組み合わせは次のように計算できます。
3人から2人選ぶ組み合わせ
\({}_3C_2=\)\({}_3P_2 \above 1pt 2! \)\(=\)\(3×2 \above 1pt 2×1\)\(=3[通り]\)
・n(全体の個数)=3
・r(選ぶ個数)=2
・n−r+1(最後の数)=3-2+1=2
\({}_3C_2=\)\({}_3P_2 \above 1pt 2! \)\(=\)\(3×2 \above 1pt 2×1\)\(=3[通り]\)
・n(全体の個数)=3
・r(選ぶ個数)=2
・n−r+1(最後の数)=3-2+1=2
この式は、『全体が3個から2個選ぶ組み合わせ 』は、『最初が3、最後が2(=3-2+1)までの2個の掛け算(3P2)) 』を分子に、『最初が2、最後が1までの2個の掛け算(2!)』を分母にした割り算により『3通り』と求められることを意味しています。

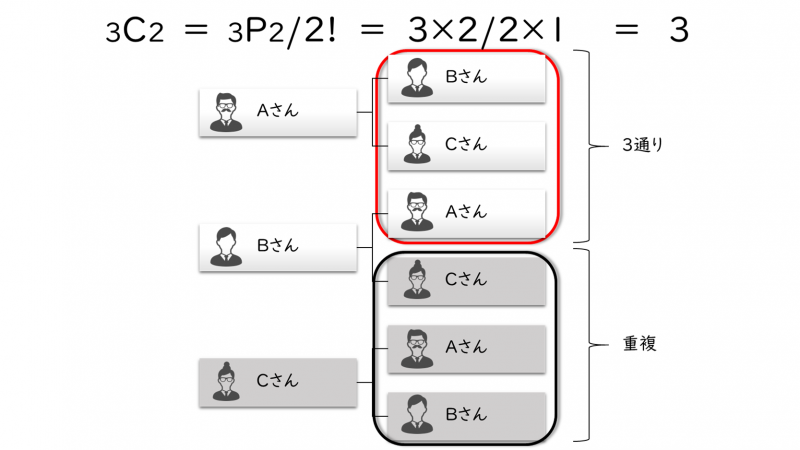
この具体例を樹形図(事柄を順番に書き出す表記法)でも確認をしておきましょう。
【例題】組み合わせ
『組み合わせ』の例題で確認しておきましょう。
a、b、c、d、e、fの6文字を任意に4個選んだとき、aとbが選ばれるのは、何通りか。
【解答・解説】
選んだ4個には、aとbが含まれるので、『a、b、?、?』になる。つまり、『?、?』の組み合わせを考えればよい。
選んだ4個には、aとbが含まれるので、『a、b、?、?』になる。つまり、『?、?』の組み合わせを考えればよい。
c、d、e、fの4個から2個選ぶ組み合わせを計算すると、
4C2=4×3/2×1=12/2=6
したがって、6通り
【まとめ】確率と統計(組み合わせ)
それでは、最後におさらいをしておきましょう!




.png)
コメント