集合とは?
集合とは、ある条件に基づいたデータ(物事)の集まりです。
例えば、『食べ物』の条件の集合を考えてみます。『食べ物』の集合には、パンやみそ汁、牛乳…等が含まれます。
ベン図とは?
ベン図は、集合の関係を視覚的に図示する表記法です。
具体的に、食べ物の集合で、『固形』の食べ物を集合A、『液体』の食べ物を集合Bとします。この集合は、ベン図により次のように表記できます。
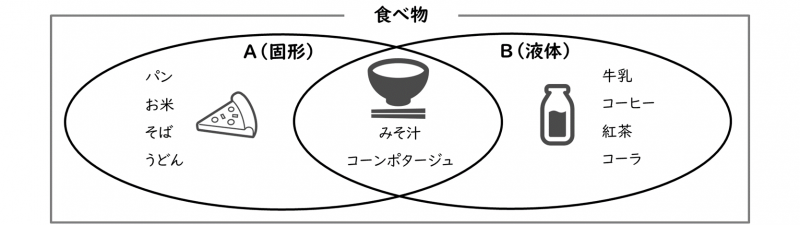
『食べ物』の集合のうち、『固形』と『液体』の集合AとBの領域、さらに『液体かつ固体』の食べ物である集合AとBの重なった領域の関係性がベン図で視覚的に理解できます。
和集合/積集合/否定
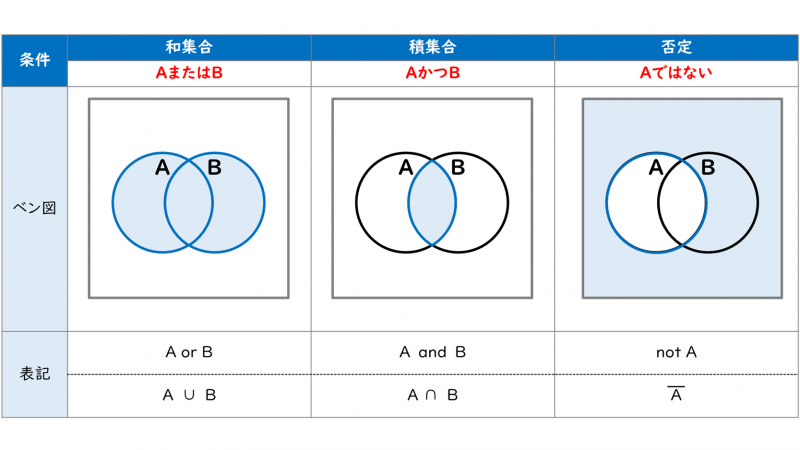
複数の集合による条件の表現として、和集合、積集合、否定があります。ここでは、先ほどから引き続きに集合Aと集合Bの2つの集合で解説していきます。
和集合
和集合は、『AまたはB』の集合です。式で表すと『A or B』、『A ∪ B』と書きます。
※∪:cop[コップ]
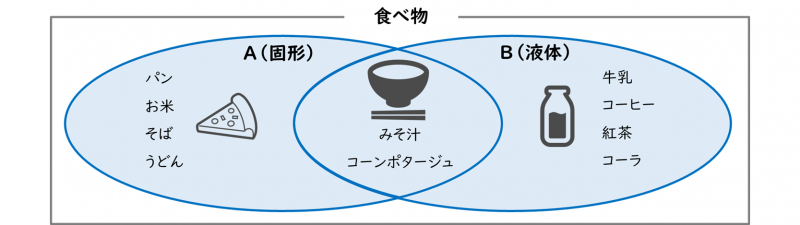
『A(固形)』と『B(液体)』の和集合は、『A(固形)』または『B(液体)』の集合です。つまり、ベン図では、『A(固形)』と『B(液体)』の全領域の集合を表します。
積集合
積集合は、『AかつB』の集合です。式で表すと『A and B』、『A ∩ B』と書きます。
※∩:cap[キャップ]
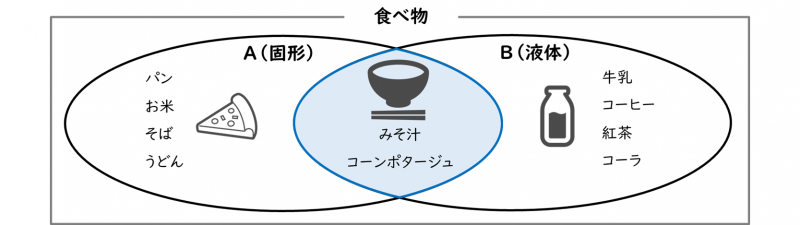
『A(固形)』と『B(液体)』の積集合は、『A(固形)かつB(液体)』の集合です。ベン図では『A(固形)』と『B(液体)』の重なった部分の集合になります。
否定
否定は、『Aでない』集合のことです。式で表すと、『not A』、『\(\bar A\)』と書きます。
※ー:bar[バー]
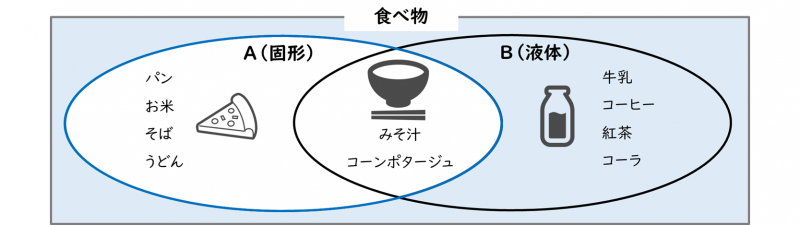
『A(固形)』の否定は、『A(固形)』の領域ではない部分の集合です。
【まとめ】集合(和集合/積集合/否定)とベン図
それでは最後におさらいをしておきましょう。
| 用語 | 説明 |
|---|---|
| 集合 | ある条件に基づいたデータ(物事)の集まり |
| ベン図 | 集合の関係を視覚的に図示する表記法 |
| 和集合 | AまたはBの集合のこと、『A or B』、『A ∪ B』と表記 |
| 積集合 | AかつBの集合のこと、『A and B』、『A ∩ B』と表記 |
| 否定 | Aではないの集合のこと、『not A 』、『\(\bar A\) 』と表記 |
※(Aバー):\(\bar A\)




コメント