アルゴリズムとは?
アルゴリズムとは、目的を達成するための処理手順のことです。
例えば、1から3までの整数を合計する目的の場合、次のような処理手順が考えられます。
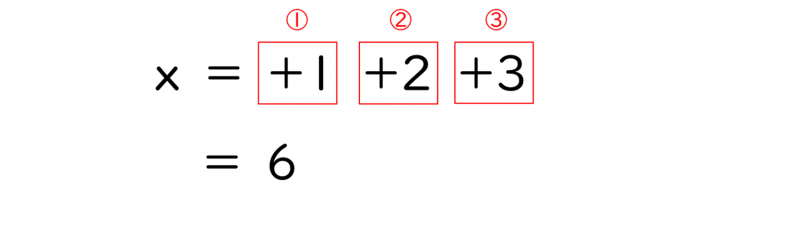
| 番号 | 処理 |
|---|---|
| ① | xに1を足す |
| ② | xに2を足す |
| ③ | xに3を足す |
流れ図(フローチャート)とは?
流れ図(フローチャート)とは、アルゴリズムを視覚的に表現する表記法です。次表の意味を持つ記号で記述します。
の記号-800x225.png)
次に解説するアルゴリズムの基本構造で、流れ図(フローチャート)を確認していきます。
アルゴリズムの基本構造(順次/繰返し/選択構造)
アルゴリズムの基本構造として、『順次構造』、『繰返し構造』、『選択構造』があります。
| 用語 | 説明 |
|---|---|
| 順次構造 | 処理を順番にするアルゴリズムの基本構造 |
| 繰返し構造 | 条件が満たされるまで、処理を繰り返すアルゴリズムの基本構造 |
| 選択構造 | 条件によって処理を選択するアルゴリズムの基本構造 |
「1~3までの整数の合計を求めるアルゴリズム」を例に、各基本構造を流れ図を用いて説明していきます。
順次構造
順次構造とは、順番に処理するアルゴリズムの基本構造です。
ここで、「1~3までの整数の合計を求めるアルゴリズム」の順次構造を流れ図で表記してみます。
-800x450.png)
| 番号 | 処理 |
|---|---|
| ① | xに0を代入(x=0) |
| ② | xに1を足す(x=0+1=1) |
| ③ | xに2を足す(x=1+2=3) |
| ④ | xに3を足す(x=3+3=6) |
流れ図では、アルゴリズムの始めと終わりを、端子という記号で挟み、各記号は流れ線で結びます。さらに、順次構造では、開始の端子から処理の記号をもちいて、一つ一つ処理を記述します。
繰返し構造
繰返し構造とは、条件が満たされるまで処理を繰り返していくアルゴリズムの基本構造です。
繰返し構造を用いて、「1~3までの整数の合計を求めるアルゴリズム」を流れ図で記述します。
-800x450.png)
| 番号 | 処理 |
|---|---|
| ① | nに1、xに0を代入 (n=1、x=0) |
| ② | [ループ1回目] xにnを足す(x=0+1=1) nに1を足す(n=1+1=2) [ループ2回目] xにnを足す(x=1+2=3) nに1を足す(n=2+1=3) [ループ3回目] xにnを足す(x=3+3=6) nに1を足す(n=3+1=4) n(=4)>3なので、ループ終了 |
繰返し構造の流れ図では、ループ端と呼ばれる記号を用います。ループ端は繰り返しの始めと、終わるための条件が記載されています。ここでは、n>3を判断の条件とし、真の場合は、アルゴリズムが終了します。偽の場合は、ループ端の間の処理を再度実行します。
選択構造
選択構造とは、条件によって処理を選択する構造です。同じく、流れ図で記述します。
-800x450.png)
| 番号 | 処理 |
|---|---|
| ① | nに1、xに0を代(n=1、x=0) |
| ② | [ループ1回目] xにnを足す(x=0+1=1) nに1を足す(n=1+1=2) [ループ2回目] xにnを足す(x=1+2=3) nに1を足す(n=2+1=3) [ループ3回目] xにnを足す(x=3+3=6) nに1を足す(n=3+1=4) n(=4)>3なので、ループ終了 |
選択構造では判断の端子に条件を記述します。ここでは、n>3を判断の条件とし、真の場合は、アルゴリズムを終了します。偽の場合は、「x+n→x」に戻ります。
基本的なアルゴリズム 探索/併合(マージ)/整列(ソート)
データを操作の基本的なアルゴリズムには、「探索」、「併合(マージ)」「整列(ソート)」があります。
、整列(ソート)-800x225.png)
IITパスポート試験での出題は多くありませんが、代表的なアルゴリズムなので、用語だけでも抑えておきましょう。
【まとめ】アルゴリズム(流れ図/基本構造)
それでは最後におさらいをしておきましょう。
| 用語 | 説明 |
|---|---|
| アルゴリズム | 与えられた目的を達成するための処理手順 |
| 流れ図 (フローチャート) | アルゴリズムを図として表現する記述方法 |
| 順次構造 | 処理を順番にするアルゴリズムの基本構造 |
| 繰返し構造 | 条件が満たされるまで、処理を繰り返すアルゴリズムの基本構造 |
| 選択構造 | 条件によって処理を選択するアルゴリズムの基本構造 |
| 探索 | 条件に合致するデータを探すアルゴリズム |
| 併合 (マージ) | データを一つにまとめるアルゴリズム |
| 整列 (ソート) | データの並びを整えるアルゴリズム |

.png)


コメント